PERSAMAAN LOGARITMA DAN SIFATNYA
Rumus Logaritma
ac = b → ª log b = c
Keterangan:
a = basis
b = bilangan dilogaritma
c = hasil logaritma
Sifat Logaritma
| ª log a = 1 |
| ª log 1 = 0 |
| ª log aⁿ = n |
| ª log bⁿ = n • ª log b |
| ª log b • c = ª log b + ª log c |
| ª log b/c = ª log b – ª log c |
| ªˆⁿ log b m = m/n • ª log b |
| ª log b = 1 ÷ b log a |
| ª log b • b log c • c log d = ª log d |
ª log b = c log b ÷ c log aKegunaan LogaritmaLogaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari integral. Dalam persamaan bn = x, b dapat dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi eksponensial. 1. Sains dan Teknik Dalam sains, terdapat banyak besaran yang umumnya diekspresikan dengan logaritma. Sebabnya, dan contoh-contoh yang lebih lengkap, dapat dilihat di skala logaritmik.
2. Penghitungan yang lebih mudah Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma:: Sifat-sifat di atas membuat penghitungan dengan eksponen menjadi lebih mudah, dan penggunaan logaritma sangat penting, terutama sebelum tersedianya kalkulator sebagai hasil perkembangan teknologi modern. KalkulusTurunan fungsi logaritma adalah dimana ln adalah logaritma natural, yaitu logaritma yang berbasis e. Jika b = e, maka rumus di atas dapat disederhanakan menjadi Integral fungsi logaritma adalah Integral logaritma berbasis e adalah Sebagai contoh carilah turunan Persamaan LogaritmaPersamaan logaritma adalah persamaan yang peubahnya terdapat dalam bilangan pokok atau numerusnya. Contoh : (i) log (3x – 1) = log (x – 15) , (ii) (x-1)log 16 = 2, dll Macam-macam bentuk persamaan logaritma :
Bentuk persamaan logaritma pada umumnya belum sederhana. Untuk menyeder- hanakan persamaan logaritma perlu memperhatikan sifat-sifat logaritma berikut : Dalam menyelesaikan persamaan logaritma, bilangan pokok logaritma perlu disamakan dahulu. Nilai penyelesaian yang diperoleh perlu diuji dengan mensubstitusikan ke persamaan semula. Nilai penyelesaian yang menjadi anggota himpunan penyelesaian (HP) adalah yang mengakibatkan :
Contoh soal Tentukan himpunan penyelesaian dari 2log (2x+1) = 3 ! Jawab: Fungsi LogaritmaFungsi Logaritma adalah suatu fungsi invers (balikan) dari fungsi eksponen. Bila fungsi eksponen dinyatakan dengan f(x) = ax, a > 0, a ≠ 1, maka invers dari f(x0 ditulis dengan f-1(x) = alog x atau f(x) = alog x, a > 0, a ≠ 1. |

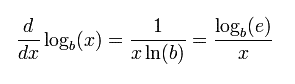
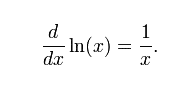
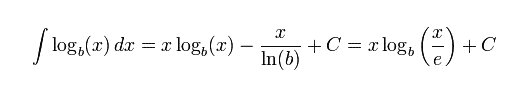
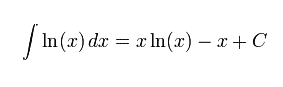
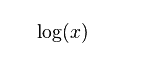
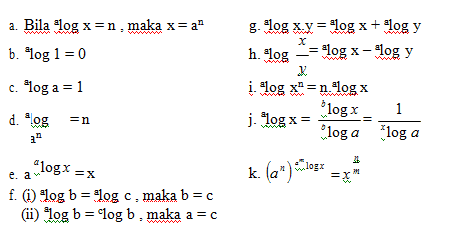

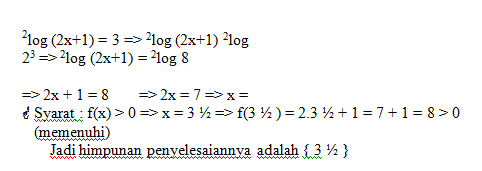


Komentar
Posting Komentar