PERTIDAKSAMAAN EKSPONEN DAN SIFATNYA

Pertidaksamaan Eksponen

Dalam bentuk pertidaksamaan, sifat-sifat pertidaksamaan eksponen dapat diketahui sebagai berikut:

Untuk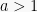 

• Jika , maka 

Contoh:

Maka:

• Jika , maka 

Contoh:

Maka:

• Jika , maka 

Contoh:

Maka:

• Jika , maka 

Contoh:

Maka:

Untuk 

Jika , maka 

Contoh:

Maka:

• Jika , maka 

Contoh:

Maka:

• Jika , maka 

Contoh:

Maka:

• Jika , maka 

Contoh:

Maka:

Rumus-Rumus Penting Pertidaksamaan Eksponen

A. Untuk $0<a<1$, jika:
   $1.a^{f\left(x\right)}<a^{g\left(x\right)}\to f\left(x\right)>g\left(x\right)$
   

$2.a^{f\left(x\right)}\le a^{g\left(x\right)}\to f\left(x\right)\ge g\left(x\right)$
   

$3.a^{f\left(x\right)}>a^{g\left(x\right)}\to f\left(x\right)<g\left(x\right)$
   

$4.a^{f\left(x\right)}\ge a^{g\left(x\right)}\to f\left(x\right)\le g\left(x\right)$

B. Untuk $a>1$, jika:
   $1.a^{f\left(x\right)}<a^{g\left(x\right)}\to f\left(x\right)<g\left(x\right)$
   

$2.a^{f\left(x\right)}\le a^{g\left(x\right)}\to f\left(x\right)\le g\left(x\right)$
  

 $3.a^{f\left(x\right)}>a^{g\left(x\right)}\to f\left(x\right)>g\left(x\right)$
   

$4.a^{f\left(x\right)}\ge a^{g\left(x\right)}\to f\left(x\right)\ge g\left(x\right)$
$aadalahbilanganpokok.$