SOAL PERSAMAAN LOAGRITMA DAN SIFATNYA
Contoh Soal dan Penyelesaiannya
1. Nilai dari 2log 4 + 2log 12 – 2log 6 =…
- 8
- 6
- 5
- 4
- 3
Pembahasan :
Untuk soal seperti di atas, maka kita perlu mengingat sifat logaritma
alog(b.c) = alog b + alog c, dan
alog = alog b – alog c
sehingga, untuk menyelesaikan soal di atas, kita gunakan kedua sifat logaritma tersebut. Dimana perhitungannya akan menjadi :
2log 4 + 2log 12 – 2log 6 = 2log
= 2log 8
Kemudian, untuk penyelesaian akhir, kita perlu mengingat sifat berikutnya, yaitu :
alog = n . alog b
→ 8 =
sehingga, penyelesaian akhirnya akan menjadi seperti berikut ini :
2log 8 = 2log
= 3 . 2log 2 → jangan lupa dengan yang ini : alog a = 1
= 3 . 1
= 3 ( E )
2. Nilai dari 2log 48 + 5log 50 – 2log 3 – 5log 2 =…
- -2
- -6
- 2
- 6
Pembahasan :
Sebelum mengerjakan, mari kita lihat perbedaan antara soal no. 1 dengan no. 2. Perbedaannya adalah :
- Pada soal no. 1, indeks logaritma merupakan indeks yang seragam ( indeks 2 )
- Sedangkan pada soal no. 2, indeks logaritma yang digunakan indeks tidak seragam ( indeks 2 dan indeks 5 )
Nah, tentu saja dengan perbedaan seperti ini, maka kita tidak bisa langsung menyelesaikannya seperti soal no. 1 di atas. Akan tetapi, soal no. 2 ini perlu di utak-atik sedikit supaya bisa diselesaikan dengan sifat-sifat yang ada.
Utak-atik yang perlu kita lakukan adalah dengan menggabungkan masing-masing logaritma dengan yang sejenis atau ber-indeks sama ( indeks 2 dengan indeks 2, indeks 5 dengan indeks 5 ), sehingga soal tersebut akan menjadi :
2log 48 – 2log 3 + 5log 50 – 5log 2 =…
Kemudian, soal tersebut bisa kita hitung dengan sifat :
alog = alog b – alog c
2log 48 – 2log 3 + 5log 50 – 5log 2 = 2log + 5log
= 2log 16 + 5log 25
Sekarang kita gunakan sifat berikutnya : alog = n . alog b
→ 16 =
→ 25 =
Dan juga gunakan sifat : alog a = 1
Sehingga, penyelesaiannya akan menjadi :
2log + 5log = 4 . 2log + 2 . 5log
= 4 + 2
= 6 ( E )
3. Jika log 3 = 0,4771 dan log 2 = 0,3010, maka nilai dari log 75 =…
- 0,7781
- 0,9209
- 1,0791
- 1,2552
- 1,8751
Pembahasan :
Untuk soal yang modelnya begini ini, ada kunci pengerjaannya yang harus kita paham. Yaitu adalah keterangan yang menunjukkan nilai log 2 dan log 3. Dengan adanya keterangan tambahan tersebut, berarti yang harus ada di pikiran kita adalah bagaimana mengubah bentuk log 75 menjadi bentuk logaritma yang mengandung unsur bilangan 2 dan 3.
→ 75 = 3 . 25 = 3 .
Sehingga, bila kita ubah bilangan 75 tersebut dengan 3. , maka akan kita dapatkan :
log 75 = log ( 3 . ) → dengan ini, kita harus ingat sifat : alog(b.c) = alog b + alog c
= log 3 + log → jangan lupa bahwa : alog = n . alog b
= log 3 + 2 . log 5
Maksudnya adalah dengan mengubah bilangan 5 pada log 5 tersebut, karena di dalam soal yang diberi keterangan adalah log 2 dan log 3, sedangkan log 5 tidak diberi keterangan apapun.
Untuk itu, trik yang perlu dilakukan di sini adalah :
→ 5 =
Bilangan 5 tersebut perlu kita ubah ke dalam suatu bilangan yang mengandung unsur bilangan 2 dan nilainya tidak berubah ( tetap bernilai 5 ). Sehingga, jika kita selesaikan, akan menjadi :
log 75 = log 3 + 2 . log → tentu masih ingat sifat alog = alog b – alog c, kan?
= log 3 + 2 ( log 10 – log 2 ) → log 10 = 10log 10 = 1 → alog a = 1
= 0,4771 + 2 ( 1 – 0,3010 )
= 1,8751 ( E )
4. Diketahui 2log 3 = 1,6 dan 2log 5 = 2,3; nilai dari 2log ..
- 10,1
- 6,9
- 5,4
- 3,2
- 3,7
Pembahasan :
Sedikit mirip dengan soal sebelumnya, dengan mengetahui ada keterangan di dalam soal mengenai nilai dari sebuah logaritma suatu bilangan, maka yang perlu kita lakukan adalah dengan mengubahnya ke dalam bentuk yang mengandung unsur bilangan yang sesuai dengan keterangan tersebut.
→ 125 = 5 . 5 . 5 =
→ 9 =
Sehingga, jika kita selesaikan soal tersebut, akan menjadi :
2log = 2log → bisa ditebak kan? Di sini kita perlu sifat : alog = alog b – alog c
= 2log – 2log
Kemudian, sifat logaritma yang kita gunakan berikutnya adalah sifat :
alog = n . alog b
maka, persamaan di atas selanjutnya akan menjadi :
= 3 . 2log 5 – 2 . 2log 3
= 3 . ( 2,3 ) – 2. ( 1,6 )
= 6,9 – 3,2
= 3,7 ( E )
5. Nilai dari 2log 8 – 1/2log 0,25 + 3log + 2log 1 =…
- -2
- -1
- 0
- 1
- 2
Pembahasan :
Pada soal kali ini, masih mirip dengan soal-soal sebelumnya. Yaitu, penyederhanaan logaritma dengan cara menggabungkan beberapa fungsi log yang memiliki indeks sama.
Jadi, untuk menggabungkan fungsi log tersebut kita harus tahu mana yang memiliki indeks yang sama.
Yang memiliki indeks yang sama adalah 2log 8; 1/2log 0,25; 2log 1
Dari ketiga fungsi log di atas, ada satu yang diwarnai merah, yaitu 1/2log 0,25 karena fungsi yang ini perlu kita ubah sedikit supaya menjadi indeks 2. Jadi, yang perlu kita lakukan adalah dengan menggunakan salah satu sifat logaritma, yaitu sifat :
Sehingga, bentuk 1/2log 0,25 bisa kita ubah menjadi
Setelah kita dapatkan bentuk sebelumnya menjadi ber-indeks 2, maka sekarang kita bisa mulai menyelesaikan soal di atas dengan menggunakan sifat-sifat dasar seperti soal sebelumnya, yaitu:
alog(b.c) = alog b + alog c, dan
alog = alog b – alog c
Sehingga, pengerjaannya akan menjadi :
2log 8 – 1/2log 0,25 + 3log + 2log 1 = 2log 8 – 2log 4 + 3log + 2log 1
= 2log + 3log
Ingat! Bahwa : =
2log 8 – 1/2log 0,25 + 3log + 2log 1 = 2log 2 + 3log → alog = n . alog b
= 1 + ( -3 )
= -2 ( A )
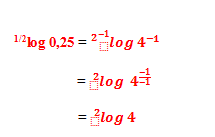


Komentar
Posting Komentar